[Aggiunta 28 maggio 2022: ho scritto la recensione completa]
Sull’Internazionale 1361 c’era un articolo sull’inferenza causale di Pearl, che avevo già sentito nominare sul blog di Gelman. Poi l’8 luglio sull’arXiv è sbucata una prepubblicazione, “Reconciling Causality and Statistics“, scritta in Inglese traballino (autori Francesi!), che mi ha fatto infine venire la curiosità di informarmi per bene su questa teoria della causalità che tutti ne parlano come se fosse il bicchiere di Gesù.
Dunque, l’articolo citava un paio di libri di Pearl: Causality (2009) e The Book of Why (2018), il primo tecnico, il secondo divulgativo. L’orgoglio mi imporrebbe di leggere direttamente i dettagli matematici, ma in realtà a me le formule fanno incrociare gli occhi se non le ho scritte io, e allora ho letto il book of why che c’ha pure un titolo più ganzo.
Il libro mi ha preso assai e pensavo di recensirlo, però l’altro ieri mentre passeggiavo nel bosco prima di cena, rimuginando su come spiegare in modo comprensibile la materia, il mio interlocutore immaginario che doveva sorbirsi le mie eccitanti spiegazioni di statistica era una femmina, sarà perché è più piacevole immaginarsi una ragazza carina che un altro studente di fisica, e a un certo punto mi si sono bloccati i pensieri perché era evidente che nelle spiegazioni non c’era nulla che potesse interessare alla donna, che anche se immaginaria e piuttosto vaga sentivo che cominciava a guardarmi con condiscendenza.
In 2 secondi ho avuto l’ispirazione di spiegare l’interpretazione causale dei paradossi di Monty Hall e Simpson (c’era nel libro) usando i peni. Poi ho pensato: i peni interessano anche ai maschi! Due piccioni con una fava. Mi ha molto divertito pensarla quindi la metto giù, la recensione del libro la scrivo poi.
Il testo seguente è un dialogo con una femmina. Se non siete una femmina, boh castratevi? Si fa per dire.
Io: Conosci il paradosso di Monty Hall?
Femmina: Sì.
Io: Risposta sbagliata, adesso te lo spiego io. C’è un gioco televisivo in cui ci sono tre porte e devi sceglierne una. Dietro a una porta c’è un’automobile, dietro alle altre ci sono delle capre. Si suppone che tu voglia vincere l’automobile e non una capra. Il conduttore (Monty Hall) ti fa scegliere una porta, facciamo che scegli la 1. Però prima di aprirla, per perder tempo, ti apre la porta 2 e dentro c’è una capra (ovviamente lui sapeva già che lì non c’è la macchina, altrimenti rovina il gioco). Allora ti chiede: «Mo’ che hai visto che la porta 2 ha la capra, tieni la 1 o cambi e scegli la 3?». Cosa ti conviene fare? Tieni la 1, passi alla 3 o è uguale?
Femmina: Ma non belano ‘ste capre? Comunque ti ho detto che lo so già, devi scegliere la 3.
Io: Ok, ma perché devi scegliere la 3?
Femmina: Elenchi tutti i casi possibili e conti quelli in cui vinci se scegli la 3, e vengono di più, bon.
Io: Va bene, ma è un paradosso perché non sarebbe la risposta intuitiva no? Quella intuitiva è che non cambia quale porta scegli, una volta che escludi la porta 2, il fatto che la 1 l’avevi scelta prima non la rende più o meno probabile della 3. E la capra è un animale silenzioso.
Femmina: Allora questi peni?
Io: Ci arrivo, prima però dobbiamo fare un diagramma causale. Considera queste tre variabili: la porta in cui c’è il premio, la porta che hai scelto, la porta che Monty Hall apre. Immagina di rappresentarle con dei pallini e di collegarli con delle frecce, ogni freccia va dalla causa all’effetto. Quindi bisogna collegare la porta del premio a quella che Monty Hall apre, perché lui non può aprire la porta con il premio, e anche la porta che hai scelto perché non può aprire nemmeno quella.
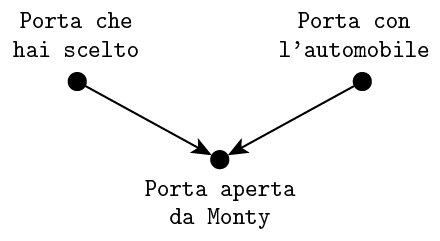
Femmina: Bene, ha disegnato le frecce (fa il gesto con le mani).
Io: Il punto di questo diagramma è che in generale quando hai due cause di una stessa variabile, e sai quanto viene la variabile, sbuca una correlazione tra le due cause anche se tra loro non c’è rapporto diretto di causalità.
Femmina: Ma allora le frecce non sarebbero al contrario? Cioè da come lo dici l’effetto ha un effetto sulla causa, non ha senso.
Io: È una cosa epistemologica, quello che sai sull’effetto ha una causa su quello che sai della causa. Cioè se trovi una bogna allora sai che ti ha punto una zanzara, però la causa è la zanzara.
Femmina: Insomma sei riuscito a dire un’ovvietà in modo incomprensibile. Epistocazzo. Ecco appunto, i cazzi?
Io: Immagina che prendo te e tua mamma
Femmina: Oh!
Io: …e vi mando in giro con un quadernino a fermare persone a caso e misurargli la lunghezza del pene. Quando li misuri tu sono in erezione, quando li misura tua mamma, no.
Femmina: Ti sei proprio sprecato. Ma non è che qualche erezione la fa venire anche mia madre? A te non piacevano le donne mature?
Io: Non c’entra, è una cosa statistica, in realtà basta che tu ne faccia venire di più della mamma. Sui vostri quadernini vi segnate la lunghezza e l’età. Poi me li portate, ricopio su excel e raggruppo per lunghezza del pene in centimetri.
Femmina: E scopri di avercelo piccolo.
Io: No, in ogni gruppo calcolo l’età media separando quelli tuoi da quelli della mamma, e viene fuori che, per qualsiasi lunghezza del pene, i tuoi sono più giovani.
Femmina: Beh grazie al cazzo devo fermare i vecchi?
Io: Ma io avevo detto di fermare persone a caso! A caso nel senso di come estrarre da un’urna, non puoi sceglierteli!
Femmina: Oh insomma te lo sei fatto tu l’esempio!
Io: Ma no, il punto è questo: da questa analisi, posso dedurre che avete contravvenuto alle mie chiarissime istruzioni scientifiche? No, perché in realtà è un paradosso equivalente a quello di Monty Hall. Il risultato che tu hai misurato persone più giovani è un’illusione statistica, è come la correlazione tra la porta che hai scelto e quella dove sta il premio. Cioè scusa l’anticorrelazione perché viene che devi cambiare porta.
Femmina: Se la porta la devo cambiare davvero, allora non è mica un’illusione.
Io: Vabbé è un’illusione nel caso dei peni, la cosa in comune tra i due esempi è che appare una correlazione inattesa. Comunque diventa chiaro se faccio il grafico:
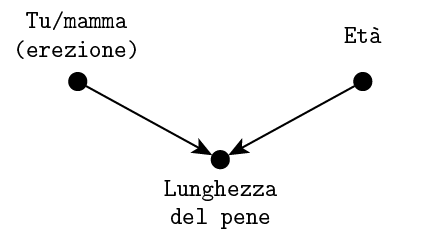
Io: Dunque, il fatto che lo misuri tu o tua madre influenza la lunghezza per via delle erezioni. Anche l’età conta perché i bimbi ce l’hanno piccolo.
Femmina: Pedofilia portami via.
Io: …Il grafico è uguale a quello di prima, e l’altra cosa in comune è che la variabile influenzata dalle altre due la fissiamo. Nel caso delle porte sappiamo qual è la porta che Monty Hall ci ha aperto, nel caso dei peni ho raggruppato i dati per lunghezza e poi faccio il conto per ogni singola lunghezza, quindi è come se fosse fissata.
Femmina: Bene, quindi la morale è che non devo giudicare i maschi in base a quanto ce l’hanno lungo.
Io: Sì ma hai capito perché viene così? Se prendi un gruppo di tizi che ce l’hanno tutti lungo uguale, ci saranno dentro un tot di bimbi e un tot di adulti. Però per avere il bimbo con il pisello lungo come l’adulto bisogna che il bimbo ce l’abbia duro e l’adulto no, e quindi sbuca questa correlazione età-erezione.
Femmina: Ok hai detto la tua perla di saggezza scientifica, però non si capisce perché devo cambiare porta con questo ragionamento.
Io: Eh allora. L’erezione e l’età hanno entrambi un effetto positivo sulla lunghezza del pene, più erezione più età pisello più lungo, e viene fuori una anticorrelazione tra le due. Invece la scelta iniziale della porta e la porta che nasconde il premio hanno un effetto negativo sulla porta aperta da Monty, perché le deve evitare entrambe. Quindi anche in questo caso viene una anticorrelazione (tra la scelta iniziale e il premio), perché due segni meno fanno più e quindi deve venire come prima. Se i segni diversi ti dan noia puoi usare “l’antierezione” e “l’antietà”.
Femmina: Ah.
