In The Book of Why, in una delle solite lagne su Rubin, Pearl si lamenta che il concetto di ignorabilità, anche se matematicamente è ben definito, non è intuitivo da capire (e quindi porta in errore chi lo deve usare in pratica per fare un’analisi). Dal capitolo 8:
But the major assumption that potential outcome practitioners are invariably required to make is called “ignorability.”
[…]
Unfortunately, I have yet to find a single person who can explain what ignorability means in a language spoken by those who need to make this assumption or assess its plausibility in a given problem. Here is my best try. The assignment of patients to either treatment or control is ignorable if, within any stratum of the confounder $Z$, patients who would have one potential outcome, $Y_x = y$, are just as likely to be in the treatment or control group as the patients who would have a different potential outcome, $Y_x = y’$. This definition is perfectly legitimate for someone in possession of a probability function over counterfactuals. But how is a biologist or economist with only scientific knowledge for guidance supposed to assess whether this is true or not? More concretely, how is a scientist to assess whether ignorability holds in any of the examples discussed in this book?
Non trovo intuitivo questo modo di spiegare l’ignorabilità con le probabilità e la stratificazione, quindi provo a usare quello che uso di solito per le relazioni di indipendenza, ovvero il trasferimento di informazioni: $A \Perp B \mid C$ vuol dire che, se so $C$, venire ulteriormente a conoscenza di $B$ non mi darebbe nessuna informazione aggiuntiva su $A$.
La relazione di ignorabilità (forte) è $\{ Y_x | x \in X \} \Perp X \mid Z$, dove $Y_x$ è il controfattuale “cosa sarebbe stato $Y$ se $X$ fosse stato $x$”. Quindi l’interpretazione informazionale è che se so $Z$, sapere quanto valeva $X$ nella realtà non mi dà nessuna informazione aggiuntiva su cosa avrebbe fatto $Y$ se $X$ fosse stato diverso.
La proprietà di essere “forte” si riferisce al fatto che tutte le $Y_x$ sono congiuntamente indipendenti da $X$, la versione debole sarebbe $\forall x: Y_x \Perp X \mid Z$. Quindi per la versione forte ho in più il vincolo che sapere il vero valore di $X$ non mi dà nessuna informazione sulla relazione che c’è tra qualsiasi insieme di $Y_x$ per diversi valori di $x$.
Esempio: al campo estivo della parrocchia, tanti anni fa, era sbucato un prete che ci aveva spiegato che Dio non ti giudica per quello che fai, ma per quello che sei. Non ricordo come avesse proseguito la supercazzola, però suppongo che il senso fosse che Dio ti può leggere alla perfezione e quindi non puoi fregarlo facendo il bravo mentre intanto pensi a come fregarlo. Non puoi “fare finta di essere buono”, per Dio questo concetto nemmeno ha senso, lui sa se sei buono o no. Puoi solo diventare buono, per andare in paradiso anziché subire una tortura eterna.
Siano $Z$ ciò che sei, $X$ ciò che fai, $Y$ andare all’inferno. Le lettere le ho assegnate per far tornare le formule di prima, perché chiaramente mi interessa $Y_x$, cioè una volta che sono all’inferno mi chiedo cosa avrei potuto fare diversamente per cambiare il giudizio divino. No dai così è troppo deprimente, facciamo che mi rimane poco da vivere, così ho un interesse un po’ più attivo in $Y_x$.
Visto che questa quantità l’ho definita “controfattuale” può a prima vista sembrare insensata se si riferisce a qualcosa nel futuro, perché di solito un controfattuale a parole si esprime come “se $X$ fosse stato…”, non se “se $X$ sarà…”. Però in realtà nel concetto formale di controfattuale non c’è alcun riferimento al tempo; difatti, nel futuro si realizzerà un certo valore di $x’$ di $X$, non sappiamo quale, e per tutti gli altri $x \ne x’$ è vero che $Y_x$ è, alla lettera, contro-fattuale. Per tradurlo in una frase, possiamo dire che $Y_x$ è il valore di $Y$ se $X$ sarà stato $x$, anche se comunque si perde la sfumatura del congiuntivo.
Una prima difficoltà nell’analizzare la situazione è che $Z$ e $X$ si influenzano a vicenda. Se una persona può cambiare nel corso del tempo, non ho semplicemente due variabili ma una sequenza. Avrei che al tempo $t$ io sono $Z(t)$, il che mi porta a compiere una certa azione $X(t+1)$ dopo una unità temporale, le cui conseguenze mi portano a diventare una persona differente $Z(t+2)$ dopo un’ulteriore unità temporale. Però, visto che sto immaginando come contesto di essere un vecchio bacucco in punto di morte, probabilmente sono troppo testardo da troppi anni perché $Z$ cambi in maniera rilevante prima dell’ultimo istante. A questo proposito, possiamo assumere che il giudizio divino non sia caotico, altrimenti non fornirebbe un insieme di incentivi efficaci e renderebbe tutta la questione religiosa una farsa.
Vediamo l’ignorabilità marginale, $\{Y_x\} \Perp X$. Parto da un’idea iniziale istintiva sul destino della tua anima in base alle tue prossime azioni (basta con la prima persona, mi sono stufato di essere quello che muore), rappresentata da una distribuzione su $\{Y_x\}$, ad esempio se $x = \text{“dai fuoco a un gatto”}$ oppure $x = \text{“picchi una vecchia a caso”}$, ho $P(Y_x) = 80\,\%$ (ricordiamo che $Y = \text{inferno}$), mentre se $x = \text{“lasci tutto in eredità alla chiesa”}$ ho $P(Y_x) = 1\,\%$.
Prima di morire vuoi prendere una boccata d’aria ed esci a fare una passeggiata con la badante. Nell’attraversare la strada, procedi in diagonale anziché ortogonalmente alla carreggiata. Giacché Nostro Signore è un DSA, come si può dedurre dalla rigidità estrema delle leggi fisiche che ha creato, questo è un peccato della peggior risma. A questo punto non posso che predirre $P(Y)=99\,\%$. Ma quello che ci interessa è: ora che ho visto la realizzazione $x’$ di $X$, come cambiano le mie opinioni su $Y_x$, cioè su cosa sarebbe successo se tu avessi agito più assennatamente?
A dare retta al prete, allora Dio non dovrebbe giudicare in base a $X$, ma secondo $Z$. D’altro canto, forse non intendeva le sue parole così letteralmente, perché trovo difficile credere che qualsiasi $X$, per quanto estremo, non abbia effetto su $Y$, se in qualche modo nella mia testa sono convinto che $Z$. Vorrebbe dire che puoi fregare Dio essendo tanto matto quanto violento. Diciamo così: il prete voleva farci capire che $Z$ è molto importante, dando per scontato che tutti avessero chiaro che comunque non si può trascurare $X$. Quindi, anche se sei una persona molto buona, se attraversi la strada in diagonale probabilmente vai all’inferno, è un atto che va oltre ogni concezione.
Tornando alla nostra inferenza, vedere quanto ti sei comportato male mi fa però supporre che probabilmente non sei neanche buono. Allora immagino che, qualunque cosa tu avessi fatto, probabilmente saresti andato comunque all’inferno perché Dio sapeva che non eri buono dentro. In simboli: $X$ mi dà delle informazioni su $Z$; visto che $Y$ dipende direttamente da $Z$, abbiamo che le probabilità degli $Y_x$ cambiano dopo aver visto $X$, anche se nei controfattuali $X$ è stata fissata a un altro valore $x$. Conclusione: $X$ non è marginalmente ignorabile, $Y_x \not\Perp X$.
Preliminari: fatti. Ora ci occupiamo dell’ignorabilità condizionale, $\{Y_x\} \Perp X \mid Z$. Questo è il punto di vista degli angeli nella bisca clandestina che stanno scommettendo su di te, facciamo che loro sanno leggere e comprendere la tua mente perché sono esseri superiori a te ma nemmeno loro sono in grado di predirre la decisione di Dio perché Egli è il più superiore di tutti, ovvero sanno $Z$ e possono condizionarsi ad essa. Inoltre, a differenza degli esseri umani, scommettono sui controfattuali, per complicate ragioni teologiche che non staremo ad approfondire. Quindi: come cambiano le puntate degli angeli sulle $Y_x$? Dati certi valori di $Z$ e $X$, gli angeli usano la loro migliore intuizione di come ragiona Dio per assegnare la probabilità di $Y$. Visto che $Z$ lo sanno, qualunque valore immaginino per $X$, la loro inferenza è determinata. Quindi, quando arriva la notizia sul tuo attraversamento, le loro predizioni controfattuali non cambiano, $P(Y_x|X,Z) = P(Y_x|Z)$. L’unica predizione che cambia è quella su $Y$, perché nella realtà andrai all’inferno giacché nella realtà hai attraversato così storto. Conclusione: $X$ è condizionalmente ignorabile dato $Z$.
Sono partito criticando Pearl, quindi per par condicio adesso riderivo la risposta usando i suoi metodi. So che $Z$ causa $X$ e $Y$, e che $X$ causa $Y$. Rappresento queste relazioni con delle frecce:
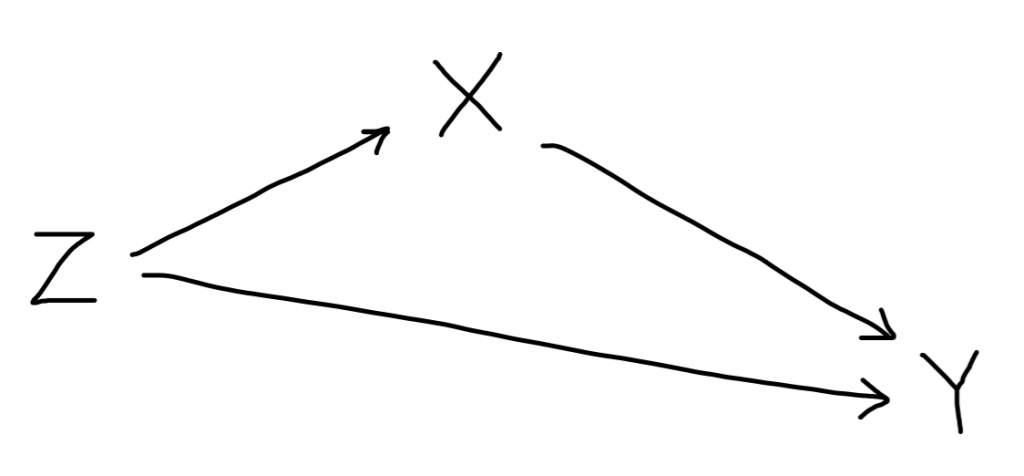
Per verificare le relazioni di indipendenza sui controfattuali, costruisco il grafo gemello:
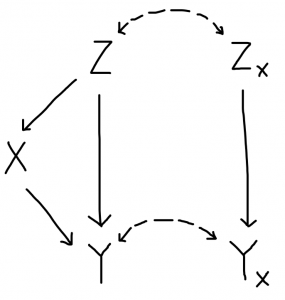
Per la d-separazione, $Y_x \not\Perp X$ (più precisamente, non posso dimostrarlo dal grafo, la d-separazione è sufficiente ma non necessaria in un SCM) perché il percorso $Y_x \leftarrow Z_x \leftrightarrow Z \rightarrow X$ è aperto. Gli altri percorsi sono bloccati dai colliders in $Y$, quindi bloccando $Z$ si ha $Y_x \Perp X \mid Z$. Per l’ignorabilità forte, duplico ulteriormente il grafo:
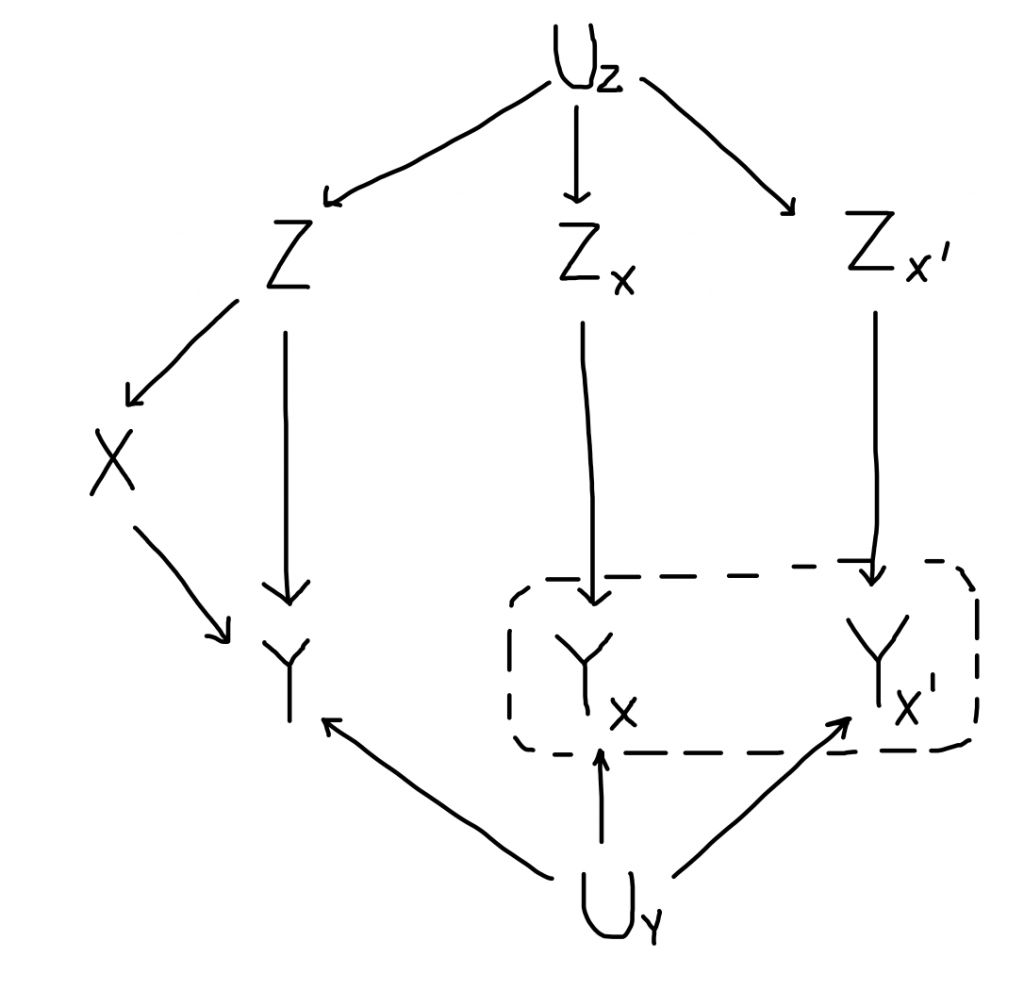
Questa volta devo rappresentare esplicitamente le variabili $U$ perché sono connesse a più di due nodi. Per gli insiemi di variabili, la d-separazione vale se vale separatamente per ogni variabile nell’insieme. Comunque come prima tutti i percorsi per arrivare a $X$ passano da $Y$ (collider, chiuso) e/o da $Z$ (aperto), quindi vale anche l’ignorabilità forte, $\{Y_x\} \Perp X \mid Z$.
Visto che duplicare tante volte tutto il grafo diventa scomodo quando ci sono tante variabili, faccio la versione compatta; Pearl non la spiega in Causality però in base alla definizione di SCM funziona. L’idea è che $Z_x = Z$, perché $X$ è a valle di $Z$, quindi non mi serve duplicarla esplicitamente:
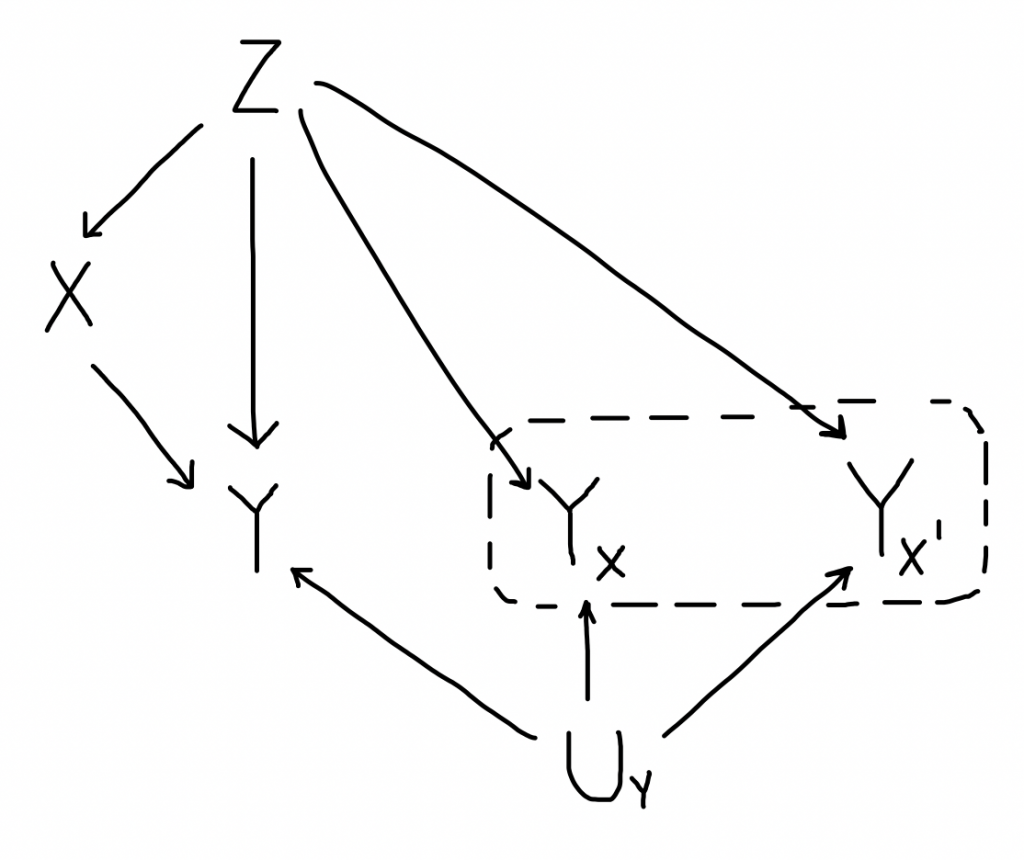
Il ragionamento funziona come prima. Credo che compattare i grafi gemelli in questo modo risolva il problema della non necessarietà della d-separazione, ma non ho controllato. Infine, ultima alternativa, gli SWIG di Richardson e Robins:
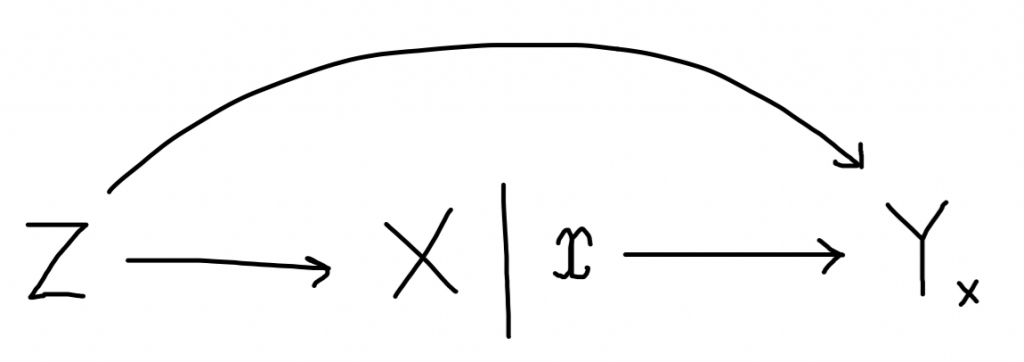
Questo è il modo più sintetico di rappresentare i controfattuali in un grafo, però posso metterci solo un $Y_x$ alla volta quindi non posso derivare relazioni di ignorabilità forte. Posso solo ricavare $Y_x \Perp X \mid Z$ perché la barra tra $X$ e $x$ indica una sconnessione e il percorso $X\leftarrow Z \rightarrow Y_x$ va bloccato.
Comunque, per un caso così semplice, Pearl dà direttamente un teorema di back-door per l’ignorabilità forte, come dice in The Book of Why, poco dopo la lamentela citata sopra:
Here is how we can use a causal diagram to test for (conditional) ignorability. To determine if $X$ is ignorable relative to outcome $Y$, conditional on a set $Z$ of matching variables, we need only test to see if $Z$ blocks all the back-door paths between $X$ and $Y$ and no member of $Z$ is a descendant of $X$.
Sono d’accordo con Pearl che sia molto intuitivo disegnare un grafo in cui le frecce rappresentano le relazioni causali ipotizzate, piuttosto che ragionare a mente su cosa è indipendente da cosa a fissato cosa. Però non mi sembra che lui si sia sforzato davvero di capire l’ignorabilità senza pensare in termini di grafi, perché io ci riesco, ho cominciato a studiare inferenza causale da poco e non credo proprio di essere più intelligente di lui. Inoltre, anche una volta che ho in mano il grafo, derivare le relazioni con la d-separazione non è immediato, bisogna imparare a farlo e stare attenti al problema che alcune indipendenze non appaiono sotto forma di separazione grafica se non sto attento con il grafo gemello, e questa cosa sui libri di Pearl non sta spiegata da nessuna parte. Quindi adesso capisco meglio perché ci sia gente che non si trova bene con i grafi e continua a scrivere tutto simbolicamente.
